how to find the equation of a parabola
The intersection of Line and Parabola Case
By Robert O
Nosotros are already enlightened of the solution of a system of two linear equations. To detect a solution to a organization of linear equations, we utilize the Gaussian elimination, algebraic substitution, or graphical method. We covered that in our previous tutorial.
How practice I solve a system of parabolic and linear equations?
What if we have one parabolic equation and the other a linear equation? We cannot utilize the Gaussian elimination in this case, but the other ii methods utilise. In this tutorial, we volition apply algebraic commutation and confirm our solution by looking at the graphs.
Line and a parabola tin either intersect at two points, one point or never intersect at all. If you lot have two solutions, and then the system intersects at two points. One solution shows that simply i intersection signal exists, and the line may be tangent to the parabola. A none solution problem ways that the line and parabola practice not meet.
Recap:
The equation of a line is of the form:
![]()
A parabolic equation takes the course:
![]()
Example 1
Solve:
![]()
![]()
Solution
The two equations are all in standard form. Then, we solve for x by equating the right sides to each other.
![]()
![]()
This is now a quadratic equation problem. By applying the formula:
![]()
Nosotros just have 1 solution for 10. Find y from the linear equation.
![]()
The line and the curve intersect at one betoken only, which is (i,-three). Let's confirm the solution past graphing them.
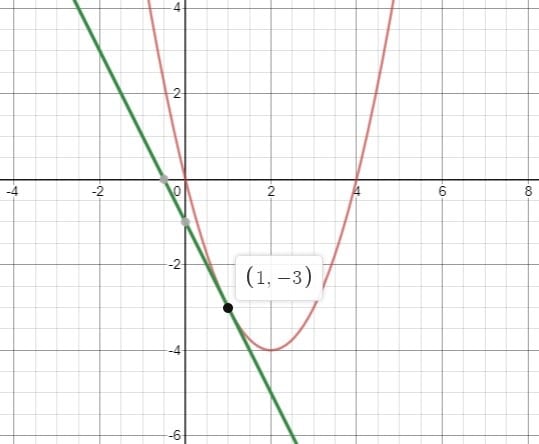
Graph generated from https://www.desmos.com/
We have only 1 solution, and we can see that the line is tangential to the parabola at (1,-3).
Example 2:
Solve
![]()
![]()
Solution
Rewriting the equation in standard class:
![]()
Equating the right side to each other:
![]()
![]()
The result is a quadratic equation. By applying the formula:
![]()
![]()
Substituting these values in the linear equation:
![]()
The parabola and the line meet at ii points (-three, iii.533) and (0.866, 1.592). Confirming our solution using a graph proves that our solutions are, indeed, correct.
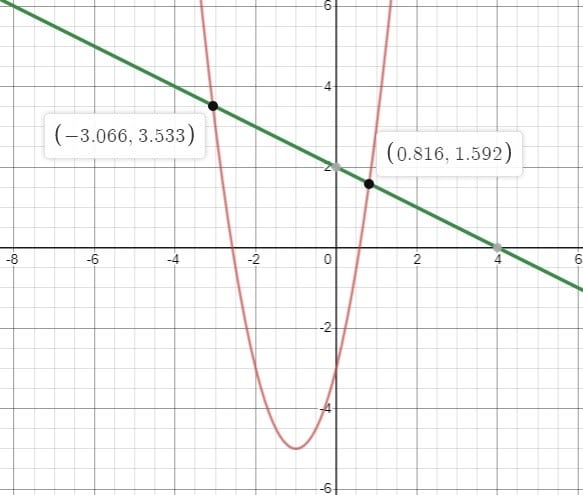
Graph generated from https://www.desmos.com/
Example 3
Solve
![]()
![]()
Solution
Nosotros start by equation the right side of both equations.
![]()
![]()
![]()
![]()
Substituting these values in the linear equation gives the values for y.
![]()
The curve and the line intersect at two points: (three,7) and (-1,-1). Graphically, we become the aforementioned solutions.
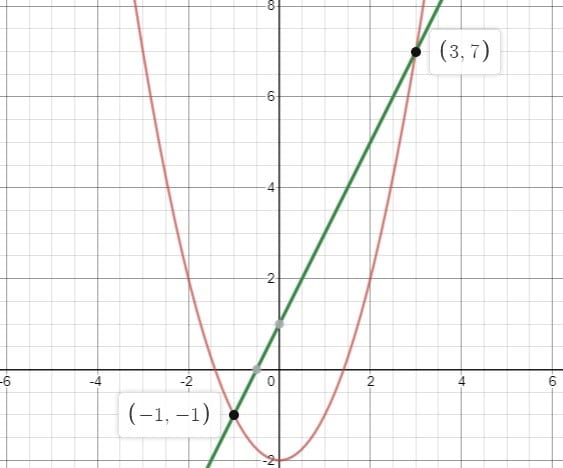
Graph generated from https://world wide web.desmos.com/
Remarks
There is no challenge in finding solutions to systems of parabolas and lines. Only rewrite the equations in standard course and equate the right sides to each other. Also, notation that you can have a parabola taking any shape. It can exist opening upwards, downward, left, or right. The line can also have either a negative or positive gradient (slope). Just solve the problem the way it is. Nothing changes.
About the Author
This lesson was prepared by Robert O. He holds a Bachelor of Engineering (B.Eng.) degree in Electric and electronics engineering science. He is a career teacher and headed the department of languages and causeless various leadership roles. He writes for Total Potential Learning Academy.
Source: https://www.fullpotentialtutor.com/how-to-find-where-a-parabola-and-a-line-intersect/
Posted by: gibbonsligine.blogspot.com

0 Response to "how to find the equation of a parabola"
Post a Comment