How To Find Distribution Of Sample Mean
6.ii: The Sampling Distribution of the Sample Hateful
- Page ID
- 570
Learning Objectives
- To learn what the sampling distribution of \(\overline{Ten}\) is when the sample size is big.
- To learn what the sampling distribution of \(\overline{X}\) is when the population is normal.
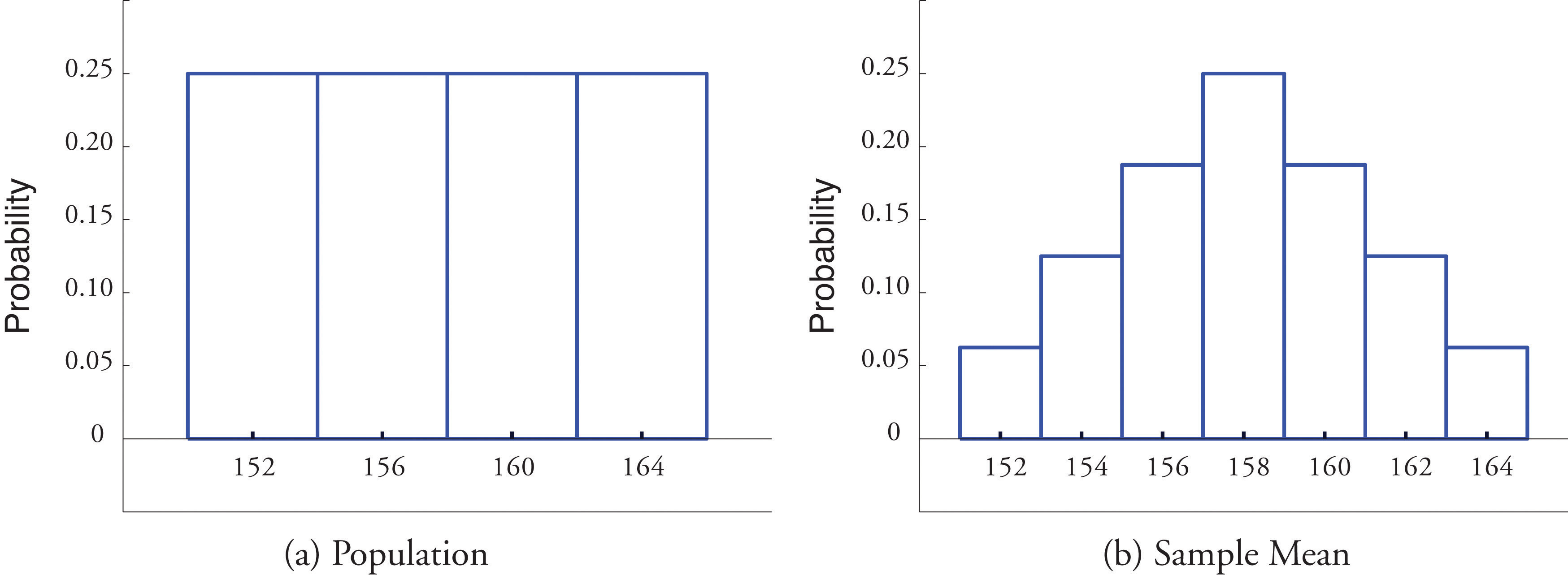
In Case 6.1.1, we constructed the probability distribution of the sample mean for samples of size ii fatigued from the population of iv rowers. The probability distribution is:
\[\begin{array}{c|c c c c c c c} \bar{x} & 152 & 154 & 156 & 158 & 160 & 162 & 164\\ \hline P(\bar{x}) &\dfrac{1}{16} &\dfrac{2}{16} &\dfrac{3}{sixteen} &\dfrac{four}{16} &\dfrac{3}{16} &\dfrac{2}{16} &\dfrac{1}{16}\\ \end{array}\]
Effigy \(\PageIndex{1}\) shows a side-past-side comparing of a histogram for the original population and a histogram for this distribution. Whereas the distribution of the population is compatible, the sampling distribution of the mean has a shape budgeted the shape of the familiar bong curve. This phenomenon of the sampling distribution of the mean taking on a bong shape fifty-fifty though the population distribution is non bell-shaped happens in general. Here is a somewhat more than realistic example.
Suppose we accept samples of size \(i\), \(5\), \(10\), or \(20\) from a population that consists entirely of the numbers \(0\) and \(1\), half the population \(0\), half \(1\), and then that the population mean is \(0.five\). The sampling distributions are:
\(north = one\):
\[\begin{array}{c|c c } \bar{x} & 0 & 1 \\ \hline P(\bar{x}) &0.5 &0.5 \\ \end{array} \nonumber\]
\(due north = 5\):
\[\begin{array}{c|c c c c c c} \bar{10} & 0 & 0.2 & 0.4 & 0.6 & 0.8 & 1 \\ \hline P(\bar{10}) &0.03 &0.16 &0.31 &0.31 &0.16 &0.03 \\ \cease{array} \nonumber\]
\(n = 10\):
\[\brainstorm{array}{c|c c c c c c c c c c c} \bar{x} & 0 & 0.1 & 0.two & 0.iii & 0.4 & 0.v & 0.vi & 0.vii & 0.eight & 0.nine & ane \\ \hline P(\bar{x}) &0.00 &0.01 &0.04 &0.12 &0.21 &0.25 &0.21 &0.12 &0.04 &0.01 &0.00 \\ \cease{array} \nonumber\]
\(n = 20\):
\[\brainstorm{assortment}{c|c c c c c c c c c c c} \bar{x} & 0 & 0.05 & 0.10 & 0.fifteen & 0.20 & 0.25 & 0.30 & 0.35 & 0.40 & 0.45 & 0.50 \\ \hline P(\bar{x}) &0.00 &0.00 &0.00 &0.00 &0.00 &0.01 &0.04 &0.07 &0.12 &0.16 &0.xviii \\ \end{array} \nonumber\]
and
\[\begin{array}{c|c c c c c c c c c c } \bar{10} & 0.55 & 0.sixty & 0.65 & 0.70 & 0.75 & 0.lxxx & 0.85 & 0.90 & 0.95 & one \\ \hline P(\bar{x}) &0.sixteen &0.12 &0.07 &0.04 &0.01 &0.00 &0.00 &0.00 &0.00 &0.00 \\ \finish{array} \nonumber\]
Histograms illustrating these distributions are shown in Figure \(\PageIndex{2}\).
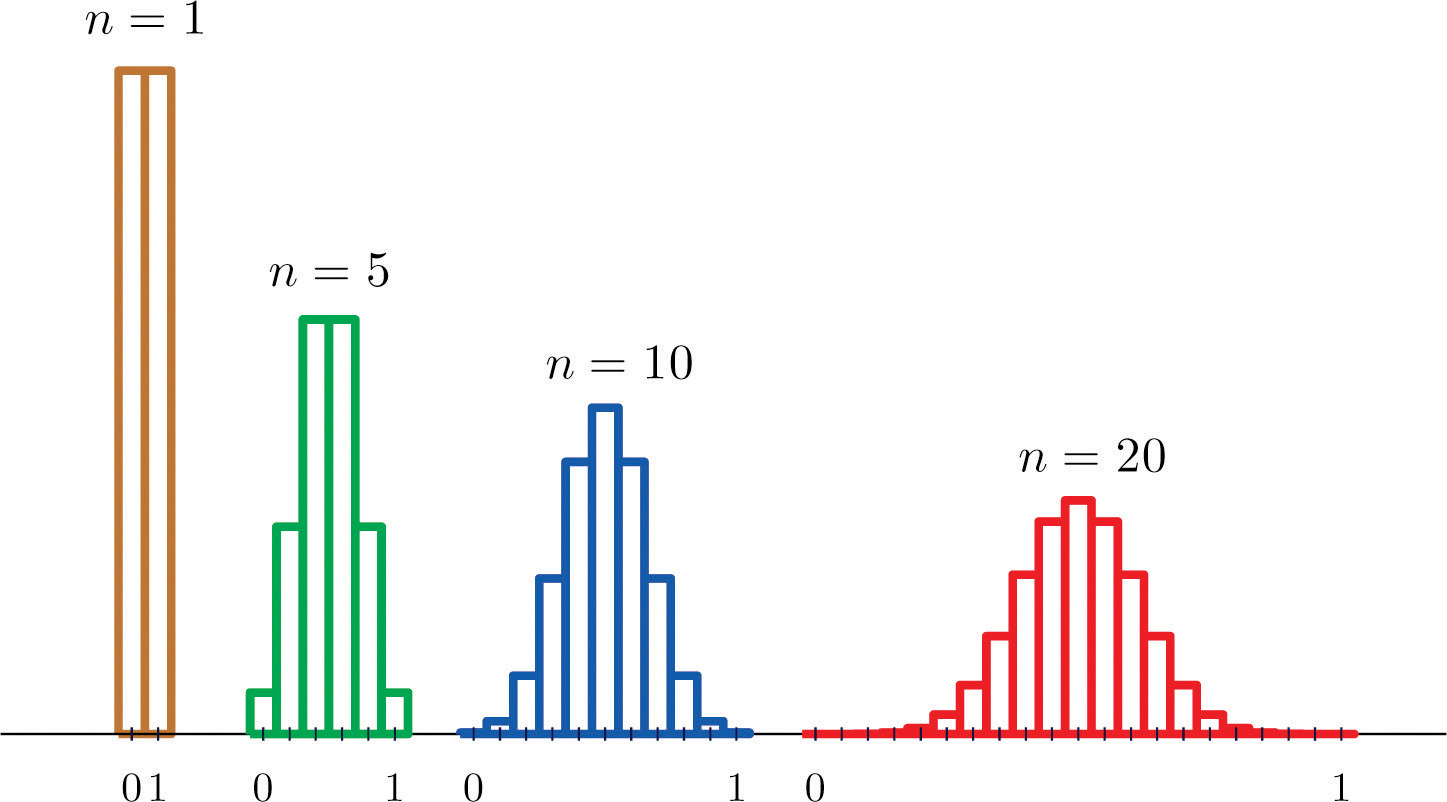
Equally \(n\) increases the sampling distribution of \(\overline{Ten}\) evolves in an interesting style: the probabilities on the lower and the upper ends shrink and the probabilities in the eye become larger in relation to them. If nosotros were to go on to increase \(n\) then the shape of the sampling distribution would become smoother and more bell-shaped.
What we are seeing in these examples does non depend on the particular population distributions involved. In general, one may start with whatsoever distribution and the sampling distribution of the sample mean will increasingly resemble the bell-shaped normal curve as the sample size increases. This is the content of the Central Limit Theorem.
The Central Limit Theorem
For samples of size \(30\) or more, the sample mean is approximately unremarkably distributed, with hateful \(\mu _{\overline{X}}=\mu\) and standard deviation \(\sigma _{\overline{X}}=\dfrac{\sigma }{\sqrt{northward}}\), where \(north\) is the sample size. The larger the sample size, the better the approximation. The Central Limit Theorem is illustrated for several common population distributions in Figure \(\PageIndex{3}\).
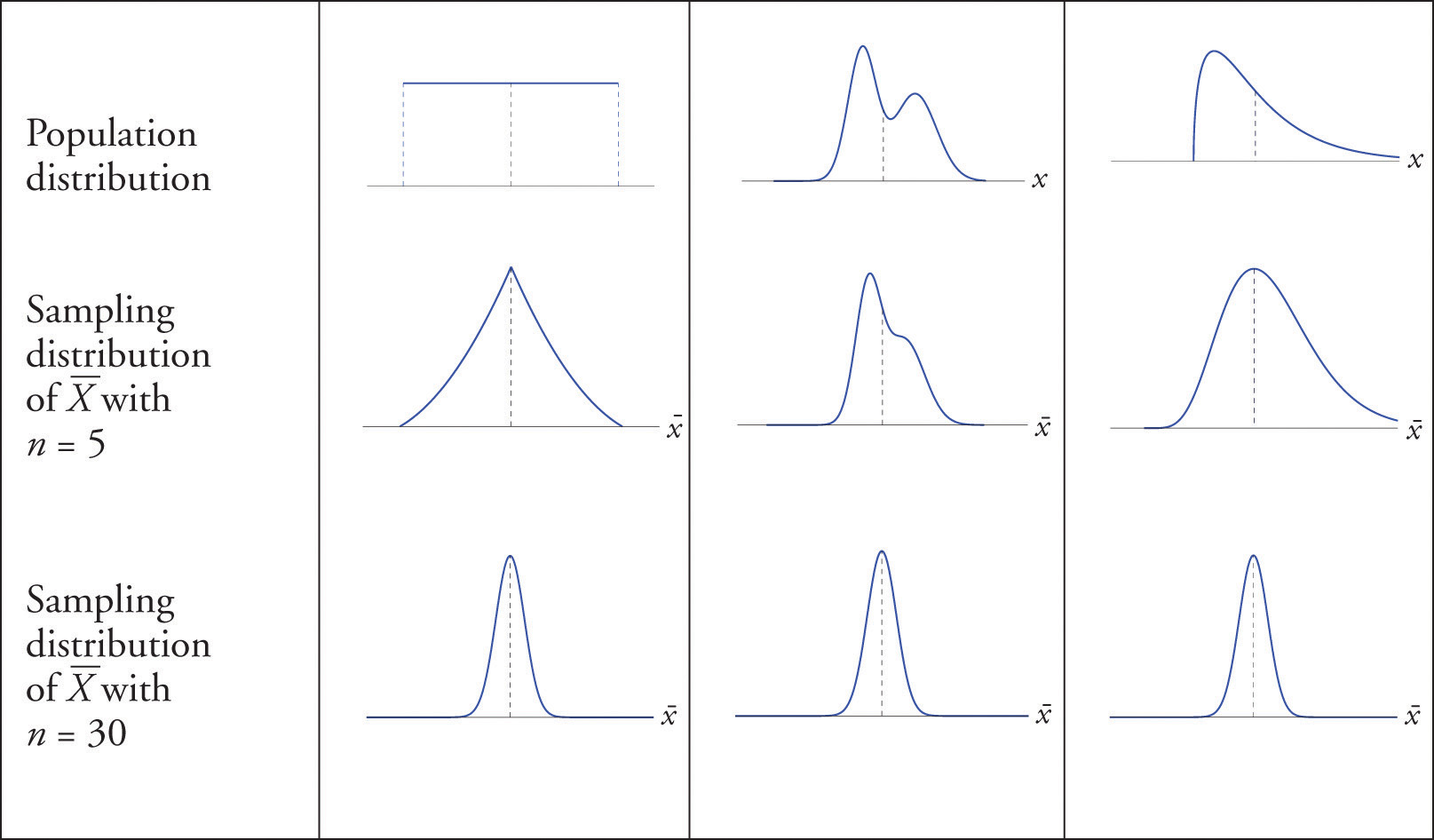
The dashed vertical lines in the figures locate the population hateful. Regardless of the distribution of the population, as the sample size is increased the shape of the sampling distribution of the sample mean becomes increasingly bong-shaped, centered on the population mean. Typically by the time the sample size is \(thirty\) the distribution of the sample hateful is practically the aforementioned as a normal distribution.
The importance of the Cardinal Limit Theorem is that it allows us to make probability statements near the sample mean, specifically in relation to its value in comparison to the population mean, every bit nosotros volition come across in the examples. Simply to employ the issue properly nosotros must first realize that there are two separate random variables (and therefore two probability distributions) at play:
- \(X\), the measurement of a single element selected at random from the population; the distribution of \(X\) is the distribution of the population, with hateful the population mean \(\mu\) and standard deviation the population standard deviation \(\sigma\);
- \(\overline{Ten}\), the mean of the measurements in a sample of size \(due north\); the distribution of \(\overline{X}\) is its sampling distribution, with hateful \(\mu _{\overline{X}}=\mu\) and standard deviation \(\sigma _{\overline{X}}=\dfrac{\sigma }{\sqrt{n}}\).
Example \(\PageIndex{1}\)
Let \(\overline{X}\) be the hateful of a random sample of size \(50\) fatigued from a population with mean \(112\) and standard deviation \(40\).
- Detect the mean and standard deviation of \(\overline{10}\).
- Notice the probability that \(\overline{X}\) assumes a value between \(110\) and \(114\).
- Detect the probability that \(\overline{X}\) assumes a value greater than \(113\).
Solution:
- By the formulas in the previous section \[\mu _{\overline{X}}=\mu=112 \nonumber\] and \[ \sigma_{\overline{X}}=\dfrac{\sigma}{\sqrt{north}}=\dfrac{forty} {\sqrt{l}}=5.65685 \nonumber\]
- Since the sample size is at to the lowest degree \(thirty\), the Cardinal Limit Theorem applies: \(\overline{X}\) is approximately normally distributed. We compute probabilities using Figure v.3.i in the usual way, only beingness careful to utilize \(\sigma _{\overline{X}}\) and not \(\sigma\) when nosotros standardize:
\[\brainstorm{align*} P(110<\overline{X}<114)&= P\left ( \dfrac{110-\mu _{\overline{X}}}{\sigma _{\overline{10}}} <Z<\dfrac{114-\mu _{\overline{X}}}{\sigma _{\overline{X}}}\right )\\[4pt] &= P\left ( \dfrac{110-112}{5.65685} <Z<\dfrac{114-112}{5.65685}\right )\\[4pt] &= P(-0.35<Z<0.35)\\[4pt] &= 0.6368-0.3632\\[4pt] &= 0.2736 \end{marshal*}\]
- Similarly
\[\begin{marshal*} P(\overline{Ten}> 113)&= P\left ( Z>\dfrac{113-\mu _{\overline{10}}}{\sigma _{\overline{X}}}\right )\\[4pt] &= P\left ( Z>\dfrac{113-112}{5.65685}\right )\\[4pt] &= P(Z>0.18)\\[4pt] &= 1-P(Z<0.xviii)\\[4pt] &= 1-0.5714\\[4pt] &= 0.4286 \end{align*}\]
Note that if in the above case we had been asked to compute the probability that the value of a single randomly selected element of the population exceeds \(113\), that is, to compute the number \(P(X>113)\), we would not take been able to do so, since we practice non know the distribution of \(10\), but only that its mean is \(112\) and its standard deviation is \(forty\). By contrast we could compute \(P(\overline{10}>113)\) even without consummate knowledge of the distribution of \(10\) because the Key Limit Theorem guarantees that \(\overline{Ten}\) is approximately normal.
Case \(\PageIndex{two}\)
The numerical population of form point averages at a college has mean \(two.61\) and standard deviation \(0.five\). If a random sample of size \(100\) is taken from the population, what is the probability that the sample mean will exist between \(ii.51\) and \(two.71\)?
Solution:
The sample mean \(\overline{X}\) has mean \(\mu _{\overline{X}}=\mu =2.61\) and standard deviation \(\sigma _{\overline{10}}=\dfrac{\sigma }{\sqrt{n}}=\dfrac{0.five}{10}=0.05\), and then
\[\begin{align*} P(2.51<\overline{X}<ii.71)&= P\left ( \dfrac{2.51-\mu _{\overline{X}}}{\sigma _{\overline{X}}} <Z<\dfrac{2.71-\mu _{\overline{X}}}{\sigma _{\overline{X}}}\correct )\\[4pt] &= P\left ( \dfrac{2.51-2.61}{0.05} <Z<\dfrac{2.71-2.61}{0.05}\right )\\[4pt] &= P(-2<Z<two)\\[4pt] &= P(Z<2)-P(Z<-2)\\[4pt] &= 0.9772-0.0228\\[4pt] &= 0.9544 \terminate{marshal*}\]
Unremarkably Distributed Populations
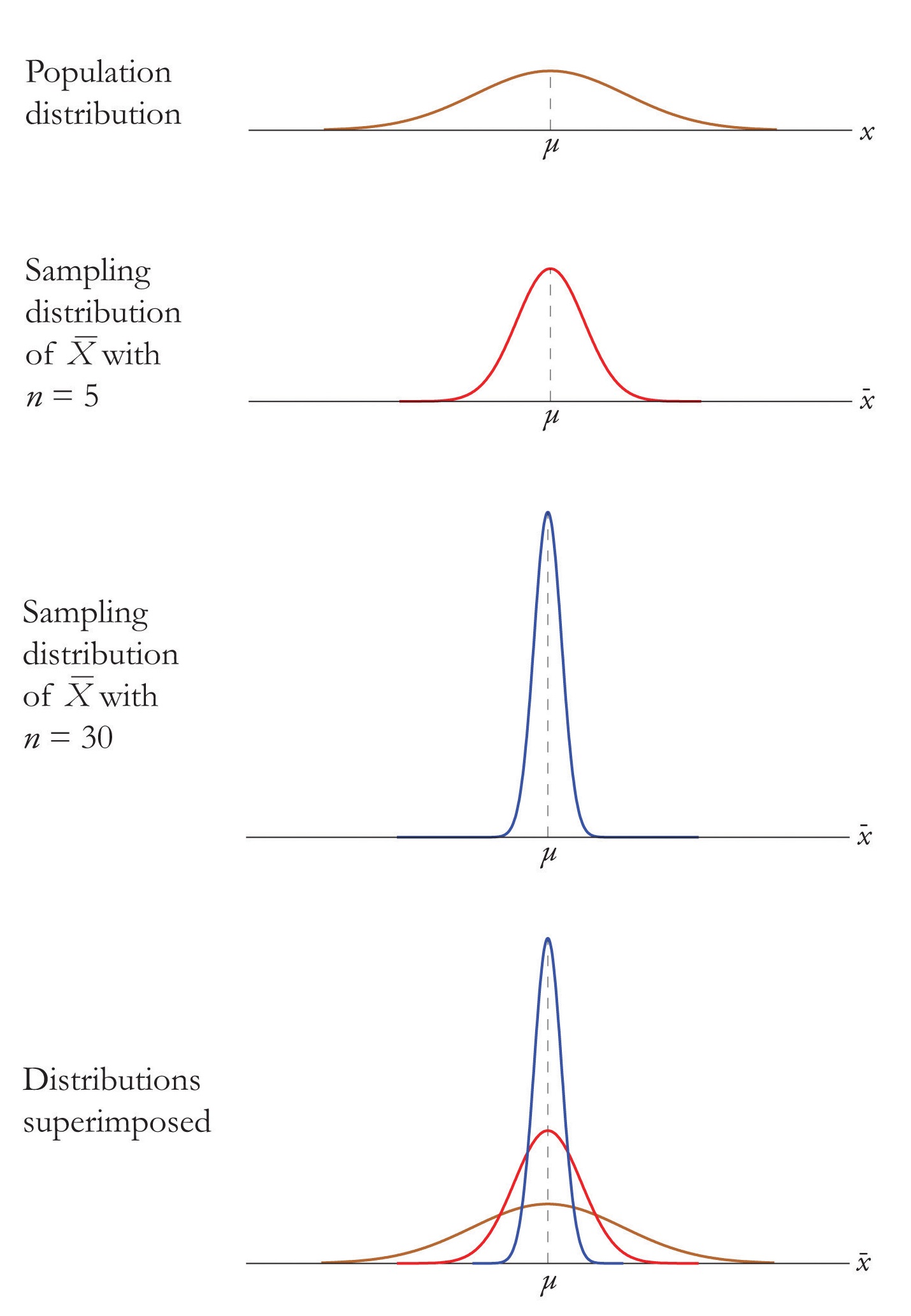
The Central Limit Theorem says that no matter what the distribution of the population is, as long as the sample is "large," meaning of size \(xxx\) or more, the sample mean is approximately unremarkably distributed. If the population is normal to begin with and so the sample mean too has a normal distribution, regardless of the sample size.
For samples of any size drawn from a normally distributed population, the sample mean is normally distributed, with mean \(μ_X=μ\) and standard deviation \(σ_X =σ/\sqrt{n}\), where \(north\) is the sample size.
The effect of increasing the sample size is shown in Figure \(\PageIndex{4}\).
Example \(\PageIndex{three}\)
A prototype automotive tire has a design life of \(38,500\) miles with a standard divergence of \(2,500\) miles. Five such tires are manufactured and tested. On the assumption that the actual population mean is \(38,500\) miles and the actual population standard departure is \(ii,500\) miles, find the probability that the sample mean will exist less than \(36,000\) miles. Presume that the distribution of lifetimes of such tires is normal.
Solution:
For simplicity we use units of thousands of miles. And then the sample mean \(\overline{Ten}\) has mean \(\mu _{\overline{X}}=\mu =38.5\) and standard deviation \(\sigma _{\overline{X}}=\dfrac{\sigma }{\sqrt{n}}=\dfrac{ii.five}{\sqrt{5}}=1.11803\). Since the population is normally distributed, so is \(\overline{X}\), hence
\[\begin{marshal*} P(\overline{X}<36)&= P\left ( Z<\dfrac{36-\mu _{\overline{X}}}{\sigma _{\overline{X}}}\right )\\[4pt] &= P\left ( Z<\dfrac{36-38.v}{i.11803}\right )\\[4pt] &= P(Z<-2.24)\\[4pt] &= 0.0125 \end{align*}\]
That is, if the tires perform as designed, in that location is only about a \(ane.25\%\) gamble that the boilerplate of a sample of this size would be so low.
Example \(\PageIndex{4}\)
An automobile bombardment manufacturer claims that its midgrade battery has a mean life of \(l\) months with a standard deviation of \(6\) months. Suppose the distribution of battery lives of this particular make is approximately normal.
- On the assumption that the manufacturer's claims are true, detect the probability that a randomly selected battery of this blazon will last less than \(48\) months.
- On the same assumption, find the probability that the mean of a random sample of \(36\) such batteries volition be less than \(48\) months.
Solution:
- Since the population is known to have a normal distribution
\[\begin{align*} P(X<48)&= P\left ( Z<\dfrac{48-\mu }{\sigma }\right )\\[4pt] &= P\left ( Z<\dfrac{48-50}{six}\right )\\[4pt] &= P(Z<-0.33)\\[4pt] &= 0.3707 \end{align*}\]
- The sample hateful has mean \(\mu _{\overline{X}}=\mu =50\) and standard divergence \(\sigma _{\overline{X}}=\dfrac{\sigma }{\sqrt{n}}=\dfrac{6}{\sqrt{36}}=1\). Thus
\[\brainstorm{align*} P(\overline{10}<48)&= P\left ( Z<\dfrac{48-\mu _{\overline{X}}}{\sigma _{\overline{X}}}\right )\\[4pt] &= P\left ( Z<\dfrac{48-l}{i}\correct )\\[4pt] &= P(Z<-2)\\[4pt] &= 0.0228 \end{align*}\]
Key Takeaway
- When the sample size is at to the lowest degree \(thirty\) the sample hateful is ordinarily distributed.
- When the population is normal the sample mean is usually distributed regardless of the sample size.
Source: https://stats.libretexts.org/Bookshelves/Introductory_Statistics/Book%3A_Introductory_Statistics_(Shafer_and_Zhang)/06%3A_Sampling_Distributions/6.02%3A_The_Sampling_Distribution_of_the_Sample_Mean#:~:text=For%20samples%20of%20any%20size,is%20shown%20in%20Figure%206.2.
Posted by: gibbonsligine.blogspot.com


0 Response to "How To Find Distribution Of Sample Mean"
Post a Comment